
Share:
Guillaume is a Senior .Net Developer Advocate for Vonage. He has been working in .Net for almost 15 years while focusing on advocating Software Craftsmanship in the last few years. His favorite topics include code quality, test automation, mobbing, and code katas. Outside work, he enjoys spending time with his wife & daughter, working out, or gaming.
The Monad Invasion - Part 1: What's a Monad?
Time to read: 9 minutes
Hey there,
During a presentation, two things can potentially make developers run away. The first is a speaker delivering a dreadfully dull presentation; the second is the mere mention of the word "Monad".
Monads have a reputation for scaring people off. Delving into Category Theory introduces a web of complex terminologies, like "Monads", making it more tricky to provide a simple and straightforward explanation.
This is the first post in a series that aims to demystify Monads and help you benefit from them, using real-life examples from our .NET SDK. Watch my related talk "Throw exceptions... out of your codebase" which was more about Monads than it was about exceptions, even if the title says otherwise.
I'm sorry to disappoint, but I won't dive into the theory aspect. I could say that a Monad is a Monoid from the category of endofunctors, but where do you go from there?
To put it simply, think of a functor as a box you can map a function over, which means you can apply a function to what's inside the box without mutating it. Now, a Monad is just a step up from a functor. It's like a super-powered box that not only allows you to map functions but also offers extra capabilities to control the sequence of operations.
Do you get it? Not yet? That's alright! We'll switch to a more pragmatic scenario for real-world examples as we delve deeper.
 An image illustrating Schrodinger's cat
An image illustrating Schrodinger's cat
Yes, this example comes from Quantum Mechanics, but there's no need to freak out, as it's relatively straightforward.
Imagine a scenario with a box and a cat. However, this isn't your typical box because it also contains a device that can release deadly poison at any moment, and you won't know when it happens.
Erwin Schrödinger's perspective is that the moment you place the cat inside the box and close it, you can't determine whether the cat is alive or dead until you open the box again. The cat isn't simultaneously dead and alive; it is either dead or alive, but you have to consider both possibilities until you can observe the actual state.
This is a way to illustrate the concept of quantum superposition where you must entertain the idea that a situation exists in multiple states until you can make an observation.
You may wonder where I'm going with all that; well, let's look at some code.
Disclaimer: no cats were harmed during the creation of these code snippets.
 An imagine illustrating cats with their thumbs Up
An imagine illustrating cats with their thumbs Up
Here's a relatively straightforward implementation of our box:
internal class SchrodingerBox
{
private readonly Cat? cat;
// Creates a box with an alive cat inside
private SchrodingerBox(Cat cat) => this.cat = cat;
// Creates a box with a dead cat
private SchrodingerBox()
{
}
// Look inside the box
public Cat? OpenBox() => this.cat;
// Shakes the box. The cat doesn't like it. Meow.
public SchrodingerBox Shake()
{
this.cat?.Meow();
return this;
}
// Shakes the box (too hard), then returns a new box with a dead cat
public SchrodingerBox ShakeTooHard()
{
this.Shake();
return new SchrodingerBox();
}
// Creates a box with a cat
public static SchrodingerBox WithAliveCat(Cat cat) => new(cat);
}
internal readonly struct Cat
{
private readonly Action<string> log;
public Cat(Action<string> log) => this.log = log;
public void Meow() => this.log("Meow");
}
I want to emphasize a few key points here:
When interacting with the public API, the only way to create a box with a living cat is by using the static factory method
.WithAliveCat(Cat).Catis a struct and, therefore, cannot be null. In this context, when the cat field is declared nullable, we understand that an instance ofCatdenotes a living cat, while null indicates that the cat has passed away.There is no direct way to inspect the cat inside the box, as no properties expose the cat's status. To determine whether the cat is alive or deceased, you must open the box using the
.OpenBox()method.
The box provides three distinct behaviours:
Shaking the box: If the cat is alive, it might not appreciate the shaking and "meows". Using the null-propagation operator ensures that we only call
.Meow()if the cat is alive. Nothing occurs if the cat is no longer among the living.Shaking the box too hard: Similar to the previous behaviour, the call will "meow" if alive. However, poison is released in this case, and the cat meets an unfortunate end.
Opening the box: By opening the box, we receive the cat, either alive (an instance) or deceased (null).
To witness the box in action, let's look at some code:
private readonly ITestOutputHelper helper;
private Cat GetAliveCat() => new(value => this.helper.WriteLine(value));
// "Meow" is logged three times in the console.
SchrodingerBox.WithAliveCat(this.GetAliveCat())
.Shake()
.Shake()
.Shake();
// "Meow" is logged twice in the console, given we killed the cat on the second call.
SchrodingerBox.WithAliveCat(this.GetAliveCat())
.Shake()
.ShakeTooHard()
.Shake();
// OpenBox() returns an instance when the cat is alive.
SchrodingerBox.WithAliveCat(this.GetAliveCat())
.Shake()
.OpenBox()
.Should()
.Be(this.GetAliveCat());
// OpenBox() returns null when the cat is dead.
SchrodingerBox.WithAliveCat(this.GetAliveCat())
.ShakeTooHard()
.OpenBox()
.Should()
.BeNull();
You'll notice that we can work with the box without needing to check the cat's state; even shaking the box when the cat is deceased doesn't lead to any consequences.
Now, that's all well and good, but in its present form, this example doesn't offer much utility. Integrating this box into your codebase won't address any real problems.
However, that doesn't mean we should discard it entirely. Currently, our box holds a cat, but Cat is just a specific structure. With the power of generics, we could swap it out for any type!
 An image illustrating a box of tea
An image illustrating a box of tea
When it comes to replacing Cat with a generic type, there's an important aspect to ponder: Shaking the box doesn't make sense anymore. What would be the purpose of such an action?
Going ahead, we will allow any value in our box - but it has to be universally helpful. We need to offer functionalities like mutating a value or transforming the value into another type.
Here's where .Map<TResult>(Func<T, TResult>) comes into play!
internal class SchrodingerBox<T> where T : struct
{
private bool IsSome { get; }
private readonly T value;
// Constructor for Some
private SchrodingerBox(T value)
{
this.value = value;
this.IsSome = true;
}
// Constructor for None
private SchrodingerBox() => this.IsSome = false;
// Applies the function on the value IF our box contains a value
public SchrodingerBox<TResult> Map<TResult>(Func<T, TResult> map) =>
this.IsSome
? Some(map(this.value))
: SchrodingerBox<TResult>.None();
// Creates a box without a value
public static SchrodingerBox<T> None() => new();
public T? OpenBox() => this.IsSome ? this.value : null;
// Creates a box with a value
public static SchrodingerBox<TResult> Some<TResult>(TResult value) where TResult : struct => new(value);
}
The Map operation represents a significant advancement, empowering us to "alter" the underlying value. Well, "alter" might not be the right term, as we're not directly modifying the value. Instead, we're using it to generate a new value placed into another container.
You can think of this operation as being similar to .Select(Func<TSource, TResult>) in LinQ.
// We start with 3 and perform three increments. The result is then 6.
SchrodingerBox<int>.Some(3)
.Map(value => value + 1)
.Map(value => value + 1)
.Map(value => value + 1)
.OpenBox()
.Should()
.Be(6);
// The box is empty, and despite three increments, the result remains null.
SchrodingerBox<int>.None()
.Map(value => value + 1)
.Map(value => value + 1)
.Map(value => value + 1)
.OpenBox()
.Should()
.BeNull();
This concept aligns with the previous .Shake() method:
When the box lacks a value, no action is taken.
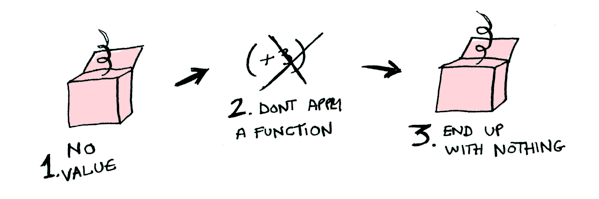 An image illustrating the None status
An image illustrating the None status
But when the box contains a value, it applies the function to that value and delivers the result in a new box.
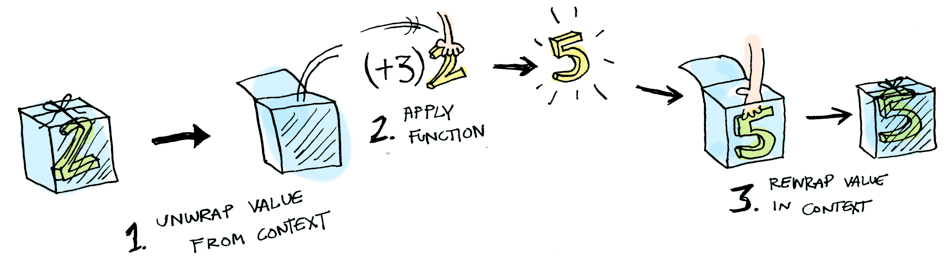 An image illustrating the Some status
An image illustrating the Some status
Source: Aditya Bhargava's blog - probably the best drawings I've seen to illustrate this mechanism
Even though we've only covered a simple transformation operation, we managed to turn our box into a Functor! Remember our earlier explanation?
"Think of a functor as a box you can map a function over, which means you can apply a function to what's inside the box without mutating the box itself."
So, what's missing for our box to evolve into a Monad?
You might have noticed that when using .Map<TResult>(Func<T, TResult>), the internal state of our box remains unchanged. Whether in a Some or None state, mapping it will preserve that state, and it's impossible to alter it.
However, this is where the Bind mechanism takes the spotlight! Unlike Map, which takes a function returning a value, the Bind method anticipates a function that returns a new box, expecting the following parameter Func<T, SchrodingerBox<TResult>>.
Let's see how it stacks up against Map:
public SchrodingerBox<TResult> Map<TResult>(Func<T, TResult> map) where TResult : struct =>
this.IsSome
// The outcome of the "map" operation is a result,
// which means we need to wrap this value within a box
? Some(map(this.value))
: SchrodingerBox<TResult>.None();
public SchrodingerBox<TResult> Bind<TResult>(Func<T, SchrodingerBox<TResult>> bind) where TResult : struct =>
this.IsSome
// The outcome of the "bind" operation is already a box,
// so, we can return it
? bind(this.value)
: SchrodingerBox<TResult>.None();
With Bind, we can implement behaviours that modify the box's state based on specific business logic. You might think: "The initial box containing the cat was already doing that, transitioning from alive to deceased" - and you're correct. However, there's a significant distinction: previously, the box held the responsibility for that change as it hosted the logic (.ShakeTooHard()). Now, the responsibility lies with the function. We successfully delegated this to the caller, expanding the possibilities of our box.
In the upcoming example, we introduce a new method, .Increment(int), which increments the value as long as it remains below three. However, if the value equals or surpasses three, it returns an empty box.
private static SchrodingerBox<int> Increment(int value) =>
value < 3 ? SchrodingerBox<int>.Some(value + 1) : SchrodingerBox<int>.None();
// We successfully incremented our value to three
SchrodingerBox<int>.Some(0)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.OpenBox()
.Should()
.Be(3);
// On the last call, our "Increment" method returns an empty box
// This signifies our box transitioned from a "Some" state to a "None" state.
// The box didn't not produce the change; the ".Increment(int)" function did.
SchrodingerBox<int>.Some(0)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.OpenBox()
.Should()
.Be(null);
Our box is finally a Monad! It now includes both Map and Bind functionalities, enabling us to manipulate a wrapped value without knowing its initial state.
However, there's still one more aspect we need to tackle.
 An image illustrating a gift box
An image illustrating a gift box
Our Monad, often known as Optional (Option or Maybe, depending on your language preference), can be in one of two states: it can represent the presence of a value (Some) or the absence of a value (None).
Currently, when we open the box, it may return null if there's no value inside. However, this doesn't align with the intent of our Monad because the absence of value is different from a null value.
This raises an intriguing question: How do you represent the absence of value? Well, you don't - instead, you provide a fallback behaviour.
And this is where .Match<TResponse>(Func<T, TResponse> some, Func<TResponse> none) comes into play!
// Applies a function depending on the state of the box to return a TResponse
public TResponse Match<TResponse>(Func<T, TResponse> some, Func<TResponse> none) =>
this.IsSome ? some(this.value) : none();
.Match(some, none) will assess the Monad's state and invoke the corresponding function.
If the state is Some, it will call
somewith the inner value to generate a result.If the state is None, it will invoke
none, relying on a fallback mechanism to generate a result.
Now, let's apply Match in place of Openboxusing the previous example:
// When the stae is Some(3)
// Match will employ the some function
// and return "The value is some 3!"
SchrodingerBox<int>.Some(0)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.Match(some => $"The value is some {some}!", () => "The value is none")
.Should()
.Be("The value is some 3!");
// When the state is None (because Bind returned an empty box in the last call),
// Match will employ the none function
// and return "The value is none"
SchrodingerBox<int>.Some(0)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.Bind(Increment)
.Match(some => $"The value is some {some}!", () => "The value is none")
.Should()
.Be("The value is none");
Initially, our box held an int. When extracting the value from the box, we focused on the "big picture" and generated a message for the end-user. Another approach could have involved providing a default int value when the state was None, assuming it would be meaningful.
The cherry on the cake: we've successfully got rid of nullability - this is always a win!
It's worth noting that the entire workflow remains consistent, whether a value is present or not. This isn't a coincidence, and I'll explore the underlying reasons later in the series.
However, this shift requires a broader consideration of the value's purpose - what are the implications of the absence of a value when nullability is no longer an option?
What does it mean in the context of an end-to-end operation?
 An image illustrating a family opening christmas gifts
An image illustrating a family opening christmas gifts
This is often the point where individuals face challenges - at least, that was the case for me - because we tend to make the rookie mistake of extracting the value prematurely.
Keeping the value inside the box makes sense as long as both states result in distinct side effects.
For instance, your monad will have a relatively brief lifespan if you can generate a value quite early, as demonstrated with the .Match(some, none) example. On the contrary, if your entire flow depends on the presence of a value, like updating a user, you will have to stick with it until the very end.
I recommend keeping your Monad active for as long as possible, extracting the value at the latest moment.
 An image illustrating traffic lights
An image illustrating traffic lights
Monads revolve around the concept of managing and manipulating states.
Obviously, our Monad is just one example among many others, each designed to handle various states. Here are a few others, along with the different states they handle:
Result (Success|Failure)
Either (Left|Right)
Validation (Success|ValidationError)
etc.
For this presentation, we developed our custom box, but it's important to note that you don't have to do the same!
There are numerous libraries available that offer ready-made Monads. Here are a few recommendations:
Language-Ext is my personal favourite, but it can be a bit overwhelming for beginners due to its extensive feature set
I hope you had fun reading this article, and I tried to make Monads less scary for you. They can be tricky when you first dive into them, but trust me, it's worth it. They changed how I approach software, and I hope they'll do the same for you.
Remember what Douglas Crockford once said: "[...] Monads are also cursed, and the curse of the Monad is that [...] once you understand, you lose the ability to explain it to anybody"
As I mentioned earlier, this blog post was just a warm-up. The topic is so vast that it won't all fit into one post, and we're about to explore some cool new stuff in the next one. So, stay tuned for that.
If you have any questions or just want to chat, feel free to hit me up on my LinkedIn or join us on the Vonage Developer Slack.
Happy coding, and catch you later!
Share:
Guillaume is a Senior .Net Developer Advocate for Vonage. He has been working in .Net for almost 15 years while focusing on advocating Software Craftsmanship in the last few years. His favorite topics include code quality, test automation, mobbing, and code katas. Outside work, he enjoys spending time with his wife & daughter, working out, or gaming.